En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números (por decir n números) es laraíz n-ésima del producto de todos los números, es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.
Por ejemplo, la media geométrica de 2 y 18 es
Otro ejemplo, la media de 1, 3 y 9 sería
![\sqrt[3]{1 \cdot 3 \cdot 9} = \sqrt[3]{27} = 3](https://upload.wikimedia.org/math/4/e/9/4e9f038c7a5c6c3b7279c56e091fa4c0.png)
- El logaritmo de la media geométrica es igual a la media aritmética de los logaritmos de los valores de la variable.
- La media geométrica de un conjunto de números positivos es siempre menor o igual que la media artimética:
Propiedades
La igualdad sólo se alcanza si 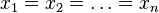 .
.
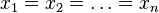 .
.![\bar{x} =
\sqrt[n]{\prod_{i=1}^n{x_i}} =
\sqrt[n]{x_1 \cdot x_2 \cdots x_n}](https://upload.wikimedia.org/math/0/4/4/044fefe7a9fb4035b5411f324535bc99.png)
![\sqrt[2]{2 \cdot 18} = \sqrt[2]{36} = 6](https://upload.wikimedia.org/math/f/d/0/fd09efd9c8e77ae938aa4ce2f7ecbcef.png)
No hay comentarios:
Publicar un comentario