sábado, 27 de junio de 2015

3.2 Desviación Media



En estadística la desviación absoluta promedio o, sencillamente desviación media o promedio de un conjunto de datos es la media de las desviaciones absolutas y es un resumen de la dispersión estadística. Se expresa, de acuerdo a esta fórmula:
D_m = \frac{1}{N} \sum_{i=1}^N \left| x_i - \overline{x} \right|
La desviación absoluta respecto a la media, D_m, la desviación absoluta respecto a la mediana, D_M, y la desviación típica,  \sigma , de un mismo conjunto de valores cumplen la desigualdad:
D_M \leq D_m \leq \sigma
Siempre ocurre
0 \leq D_m \leq \frac{1}{2} Rango
donde el Rango es igual a:
Rango = \text{valor máximo} - \text{valor mínimo}
El valor:
\, D_m = 0
ocurre cuando los datos son exactamente iguales e iguales a la media aritmética. Por otro lado:
D_m = \frac{1}{2} Rango
cuando solo hay dos valores en el conjunto de datos.
Publicado por en

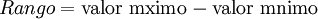
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)